DB 论文阅读：Approximate nearest neighbor algorithm based on navigable small world graphs

本文介绍向量近似最近邻（Approximate Nearest Neighbor，ANN）的一种经典算法：NSW（Navigable Small World，NSW），原文： Approximate nearest neighbor algorithm based on navigable small world graphs 。

摘要

NSW 是一种用于度量空间的近似 K 近邻算法。该算法基于图，每个向量构成顶点，向量之间的连接构成边。使用一种贪心算法的变体来进行 K 近邻查询操作；插入算法基于查询操作并连接边。插入和查询操作时间复杂度为 \({\log}^{2}(n)\)。查询和插入操作可并行执行，且该索引数据结构可分布式。无需调整索引结构即可改变 K 近邻查询正确性的概率。

1. 核心思想

索引结构是一个可导航小世界图 \(G = (V, E)\) ，向量集合 \(X\) 中的每个元素一一映射到顶点集合 \(V\) 。边集 \(E\) 由索引构造算法决定。

相关名词含义：

• 朋友（friends）：共享某条边的顶点集
• 顶点 \(v_i\) 的朋友列表：与顶点 \(v_i\) 共享一条边的顶点列表

图中的边有两个目的：

• 部分边是短程连接，用来作为 Delaunay 图的近似，以使用贪心搜索算法；
• 其余边是长程连接，用于实现对数级别复杂度的贪婪搜索。长程连负责构建图的可导航小世界属性。

数据结构示意图如下：

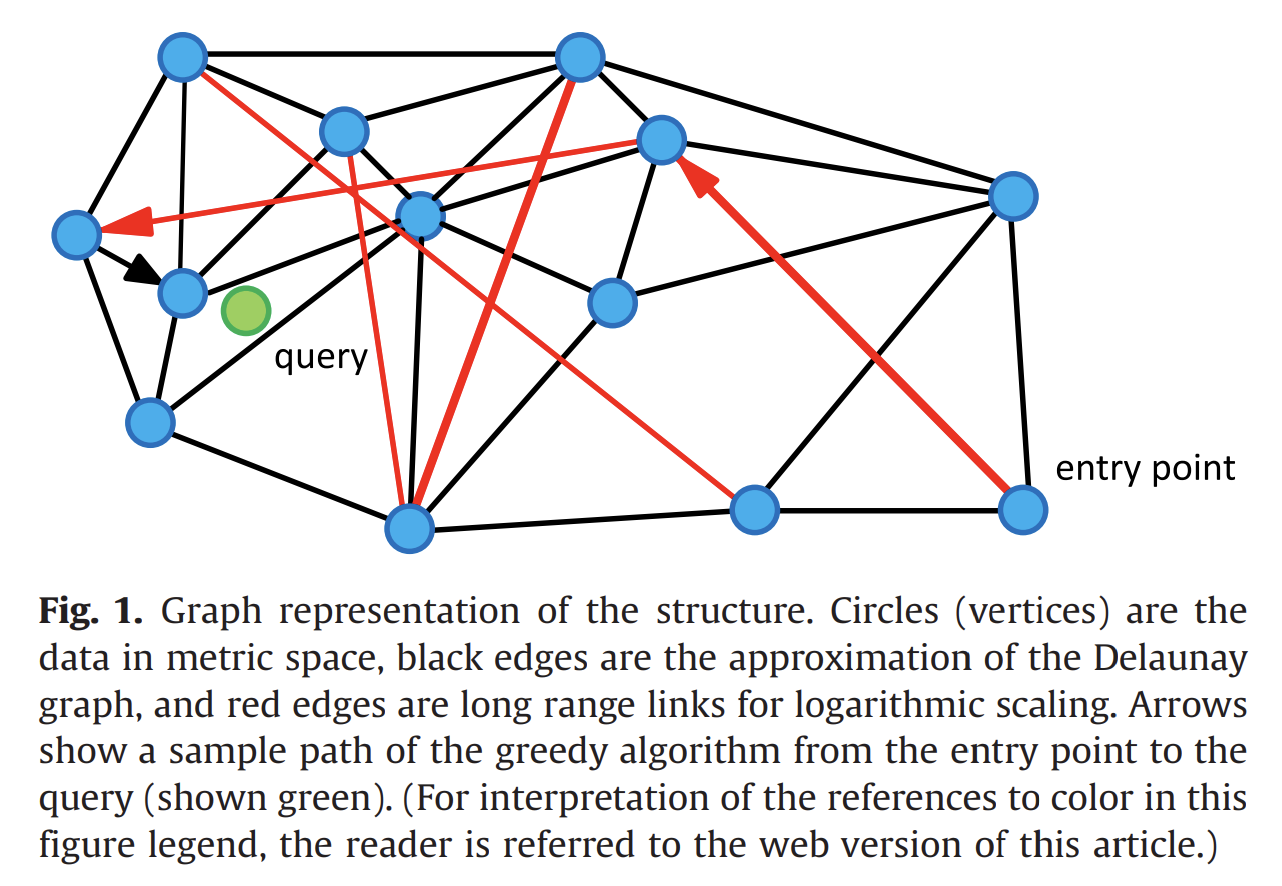
其中，蓝色圆表示图中顶点（数据集向量），绿色圆表示查询向量，黑色边是 Delaunay 图的近似（短程连接），红色边是长程连接。箭头表示从进入点（entry point）的一个贪心搜索过程。

数据结构由顶点的逐个插入形成。对于每个新加入的元素，从结构中找到其最接近的邻居集合（Delaunay 图的近似）。这个集合与插入元素相互连接。随着越来越多的元素被插入到结构中，之前作为短程连接的连接现在变成了长程连接，从而形成了一个可导航小世界图。

2. 查询算法

2.1 基本贪心查询算法

该小节的算法用于近似最近邻查询，即只返回 1 个查询结果。算法伪代码如下：

算法接收两个参数：

• \(q\) ：表示查询向量
• \(v_{entry\_point}\) ：表示查询起始顶点，且 \(v_{entry\_point} \in V\) ，即 \(v_{entry\_point}\) 是顶点集合 \(V\) 的一个元素。

执行流程如下：

从入口点开始，算法计算查询 \(q\) 到当前顶点的好友列表中每个顶点的距离，然后选择距离最小的顶点。如果查询与所选顶点之间的距离小于查询与当前元素之间的距离，那么算法会移动到所选顶点，它成为新的当前顶点。当算法达到一个局部最小值时停止，即：其好友列表中没有比该顶点更接近查询 \(q\) 的顶点。

注意，该算法并不保证返回最近邻结果，而是返回近似最近邻。

2.2 K 近邻查询

近似 K 近邻查询算法伪代码如下：

算法参数含义：

• \(q\) ：表示查询向量
• \(k\) ：即 k 近邻
• \(m\)：重复进行 \(m\) 循环体

伪代码中一些变量含义解释如下：

• 创建一个TreeSet对象tempRes，用于存储临时结果。
• 创建一个TreeSet对象candidates，用于存储当前考虑的候选顶点。
• 创建一个TreeSet对象visitedSet，用于记录已访问过的顶点，以避免重复访问。
• 创建一个列表result，用于存储最终的 k 个最近邻居。

算法主体中，外层循环即进行 \(m\) 次查询，以提高查询精度；内层循环对集合 candidates 进行动态插入及遍历，直到满足 break 条件或遍历完 candidates 结束内层循环。

3. 插入算法

插入算法伪代码如下：

参数含义：

• \(new\_object\) ：插入元素
• \(f\) ：表示进行 k 近邻查询时的参数 k
• \(w\)：表示调用 k-NNSearch 算法时的参数 \(m\)

该算法首先调用 k-NNSearch 返回近似 k 近邻结果，然后将插入元素与近似最近邻结果互相连接边。从伪代码中也可以看出索引结构是无向图。

3.1 参数选择

参数 \(w\) 决定了在构建算法中确定最近邻居的准确性（召回率）。作者建议设置足够大的 \(w\) ，以让召回率接近 1（如：0.95~0.99）。小的召回率会增加错误连接的比例，这只会提高算法的复杂性，而实验表明，插入时召回率超过 0.99 对搜索质量没有可测量的影响。测试还显示，对于最佳召回率，\(w\) 随着数据集大小的变化缓慢（对数）变化，因此，如果我们已经知道一个好的召回率的近似值 \(w0\)，我们可以首先使用大得多的 \(m\)（例如，\(m = 2\times w0 + 10\)），假设 \(m\) 足够大，使得搜索结果真正是最近的 k 个邻居，然后增加 \(w\)，并重复测试，直到达到一个高召回率（如：0.95~0.99）。操作的复杂度与数据集大小成对数关系，因此它不影响整体构建复杂度。

参数 \(f\) 决定了在插入新元素时，与新元素连接的最近邻居的数量。测试结果显示，对于维度在 1~20 的欧式空间数据，\(f\) 的值应该大约是维度 \(d\) 的 3 倍，这样可以保持内存消耗与维度线性增长，同时保持较高的搜索召回率。小的 \(f\) 能够减少单次搜索的复杂度，但是牺牲了召回质量。

4. 总结与问题

以上就是对 NSW 关键的查询、插入算法的介绍。实验部分请参考原论文。在原论文中，作者还提出了可改进的方向，以降低复杂度和/或提高准确性：

• 更复杂的节点朋友选择算法：选择最近的邻居作为朋友并不是近似 Delaunay 图的最佳方法，因为这种方法只考虑了新元素与候选节点之间的距离，而忽略了候选节点之间的距离。
• 更复杂的可导航小世界创建算法
• 更有效地管理多个搜索