DB 论文阅读:Product Quantization for Nearest Neighbor Search
本文介绍论文《Product Quantization for Nearest Neighbor Search》,即 ANN 中乘积量化(Product Quantization,PQ)算法的主要内容。
1. 背景介绍
PQ 论文在 2011 年发表于 TPAMI,是针对欧式距离设计的一种 ANN 算法。当时,基于图的算法尚未提出,主流的算法包括:Euclidean Locality-Sensitive Hashing (E2LSH)、randomized KD-trees、hierarchical k-means 等。但是,这些算法往往需要大量的内存才能运行,甚至索引结构所需要的内存超过了向量所需的内存。针对这一问题,提出了 PQ 算法。
2. 量化与乘积量化
2.1 向量量化
量化可视作信息压缩的过程。在向量量化场景下,给定量化器 \(q\),其将 \(D\) 维向量 \(x \in \mathbb{R}^{D}\) 映射到一个向量 \(q(x) \in \mathcal{C} = \{ c_i, i \in \mathcal{I} \}\) ,其中索引下标集合是有限的:\(\mathcal{I} = 0,…,k-1\) ,\(c_i\) 是中心点,\(\mathcal{C}\) 是大小为 \(k\) 的码本。被映射到同一个下标 \(i\) 的向量集合 \(\mathcal{V}_i\) 称为沃罗诺伊单元(Voronoi cell)。码本 \(\mathcal{C}\) 通常通过 k-means 算法计算得到。
2.2 乘积量化
给定一个 128 维的向量,如果使用上面的向量量化方法,假设 \(k = 2^{64}\) ,这样每个向量只需要一个 64 比特的索引即可表示。但是,由于聚类中心过多,k-means 算法时间复杂度不可接受,且存储这么多的聚类中心向量同样不现实。
解决这个问题的方法是乘积量化。给定向量 \(x\) ,将其等划分为子向量 \(u_j, 1 \leq j \leq m\) ,\(u_j\) 维度为 \(D^* = D / m\) ,其中 \(D\) 为 \(m\) 的倍数。然后,使用 \(m\) 个量化器分别对子向量进行量化,于是向量 \(x\) 映射为: \[ \underbrace{x_1, \ldots, x_{D^*}}_{u_1(x)}, \ldots, \underbrace{x_{D-D^*+1}, \ldots, x_D}_{u_m(x)} \rightarrow q_1\left(u_1(x)\right), \ldots, q_m\left(u_m(x)\right) , \] 其中,\(q_j\) 是对应第 \(j\) 个子向量的低复杂度量化器。通过子量化器 \(q_j\) ,我们将下标集合 \(\mathcal{I}_j\) 、码本 \(\mathcal{C}_j\) 和对应的重构值 \(c_{j,i}\) 联系起来。
乘积量化器的重构值可以由集合 \(\mathcal{I} = \mathcal{I}_1 \times … \times \mathcal{I}_m\) 中的一个元素表示。码本也可由笛卡尔积表示: \[ \mathcal{C} = \mathcal{C}_1 \times … \times \mathcal{C}_m , \] 集合的中心由 \(m\) 个子量化器的中心拼接得到。假设每个子量化器都有有限个(\(k^*\))重构值,于是总的中心数量为: \[ k = (k^{*})^m . \] 对比 k-means、HKM 和 乘积量化码本占用的内存和任务复杂度:
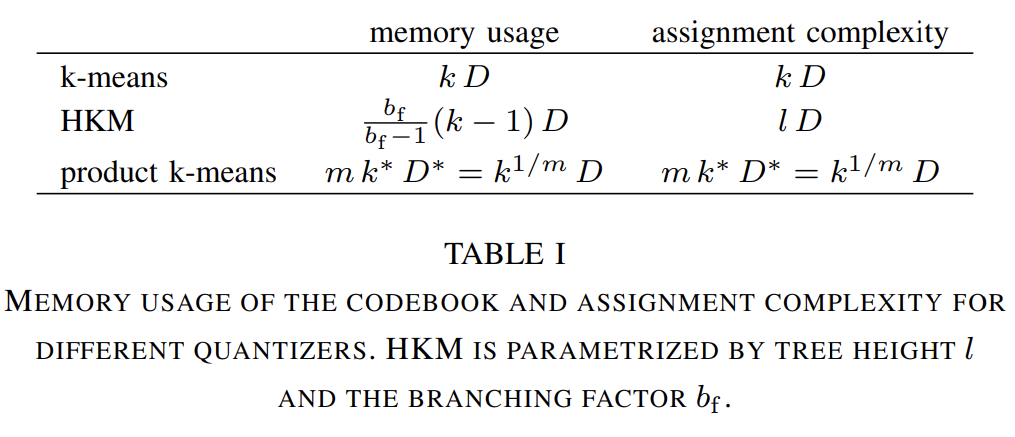
可以看出,只有乘积量化适用于 \(k\) 非常大的情况。
\(k^*\) 和 \(m\) 的取值会影响计算复杂度和量化效果,推荐的取值为:\(k^* = 256, m = 8\) 。
3. 使用量化搜索
3.1 使用量化编码计算距离
假设有查询向量 \(x\) 和数据库中向量 \(y\) ,有两种方法计算其之间的近似欧氏距离,如下图所示:
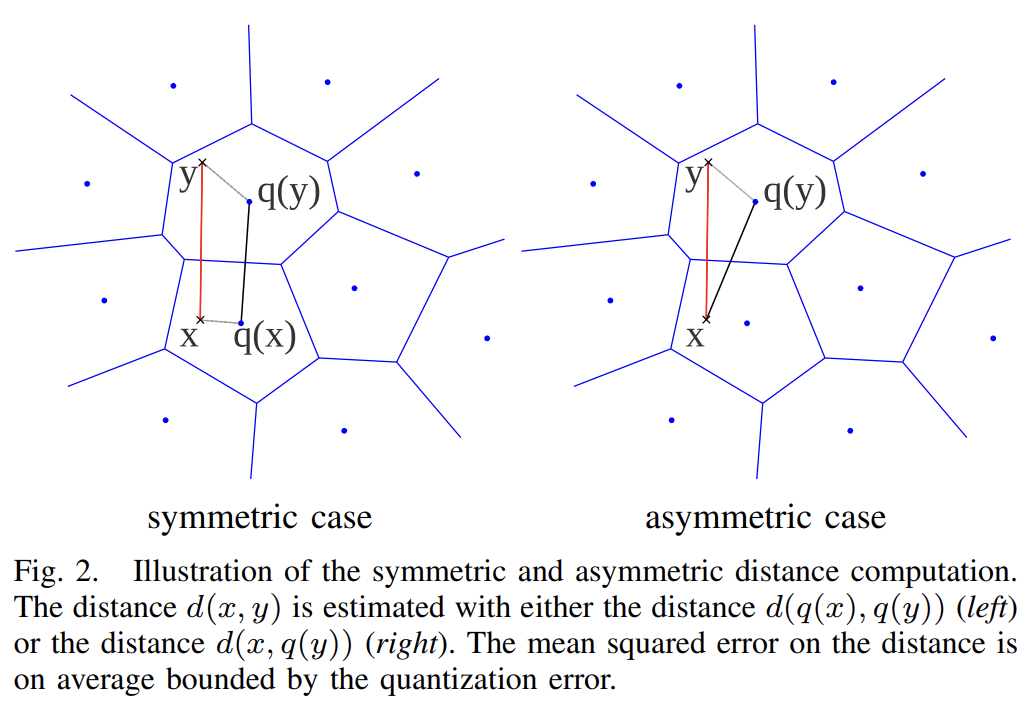
对称距离计算(Symmetric distance computation,SDC)
向量 \(x\) 和 \(y\) 都由其聚类中心 \(q(x)\) 和 \(q(y)\) 表示,即: \(d(x,y) \triangleq d(q(x),q(y))\) 。
非对称距离计算(Asymmetric distance computation,ADC)
查询向量 \(x\) 不经过量化,即:\(d(x,y) \triangleq d(x,q(y))\) 。
下表总结了在具有 \(n\) 个向量的数据集中搜索向量 \(x\) 的 \(k\) 近邻的不同步骤复杂度:

3.2 距离误差分析
在 3.1 小节中计算的距离 \(\tilde{d}(x, y)\) 与真实距离 \(d(x, y)\) 之间存在误差,此小节分析了误差界。
使用 MSE( mean squared error)评估量化器的距离误差,有 mean squared distance error (MSDE) 为: \[ \operatorname{MSDE}(q) \triangleq \iint(d(x, y)-\tilde{d}(x, y))^2 p(x) d x p(y) d y \] 又根据三角不等式: \[ d(x, q(y))-d(y, q(y)) \leq d(x, y) \leq d(x, q(y))+d(y, q(y)) \text {, } \] 其等价于(上述不等式右侧两项移项加平方可得): \[ (d(x, y)-d(x, q(y)))^2 \leq d(y, q(y))^2 . \] 将此不等式与 MSDE 联合,得: \[ \begin{aligned} \operatorname{MSDE}(q) & \leq \int p(x)\left(\int d(y, q(y))^2 p(y) d y\right) d x \\ & \leq \operatorname{MSE}(q) . \end{aligned} \] 这个不等式表明,距离误差的统计上界等于量化器的 MSE。
3.3 距离平方估计
由于使用了 \(\tilde{d}\) 或 \(\hat{d}\) 来估计距离 \(d\),很明显可以看出,估计的距离是小于真实的距离的。以 SIFT 数据集为例,如下图所示:
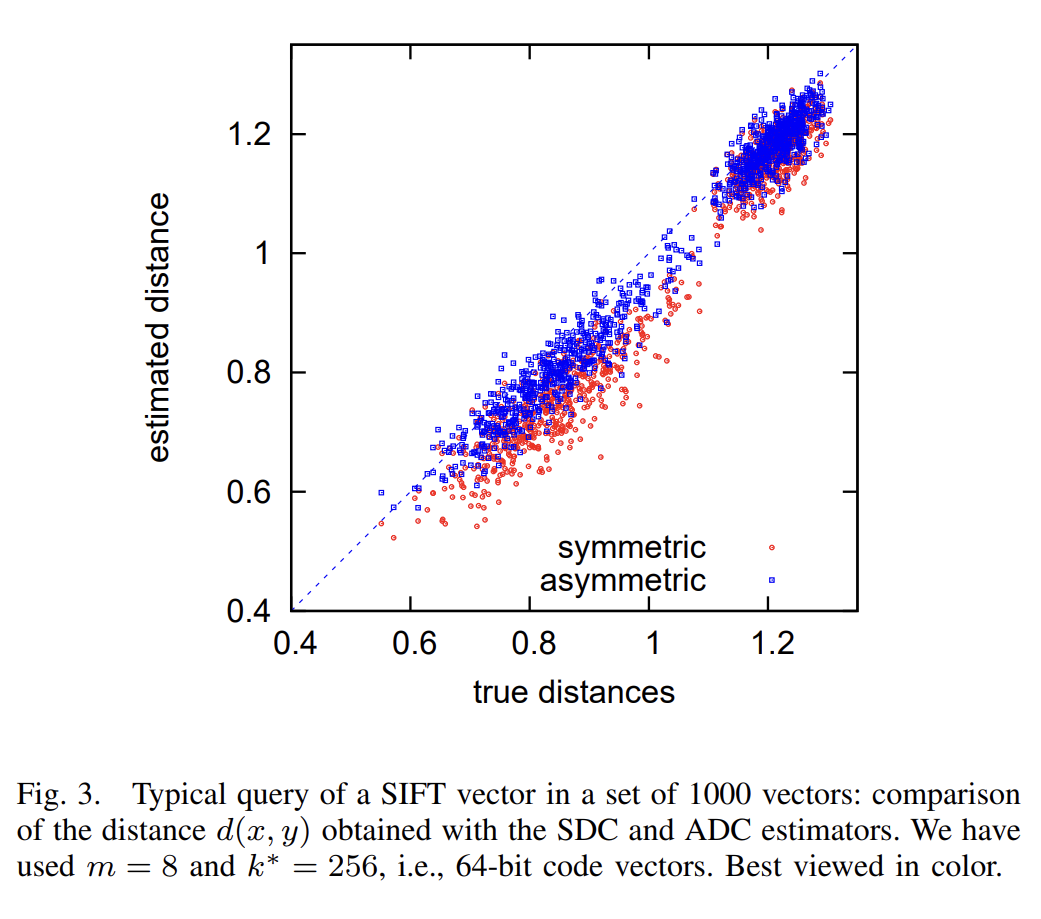
大部分点是落于直线 \(y = x\) 的下方的,且对称版本的距离误差要比非对称的更大。那么,我们应该如何更好地估计距离,以消除上述公式计算的偏差呢?
首先计算距离平方的期望 \(\tilde{e}(x, q(y))\) : \[ \begin{aligned} \tilde{e}(x, y) & \triangleq \mathbb{E}_Y\left[(x-Y)^2 \mid q(Y)=c_i\right] \\ & =\int_{\mathcal{V}_i}(x-y)^2 p(y \mid i) d y, \\ & =\frac{1}{p_i} \int_{\mathcal{V}_i}\left(x-c_i+c_i-y\right)^2 p(y) d y . \end{aligned} \] 其中 \(Y\) 为随机变量,且 \(q(Y)=q(y)=c_i\) 。由于一个沃罗诺伊单元满足以下条件: \[ \int_{\mathcal{V}_i}\left(y-c_i\right) p(y) d y=0 \] 则前面式子可简化为: \[ \begin{aligned} \tilde{e}(x, y) & =(x-q(y))^2+\int_{\mathcal{V}_i}(q(y)-y)^2 p\left(y \mid y \in \mathcal{V}_i\right) d y \\ & =\tilde{d}(x, y)^2+\xi(q, q(y)) \end{aligned} \] 又对乘积量化,量化器由多个子量化器组成,于是有: \[ \tilde{e}(x, y)=\tilde{d}(x, y)^2+\sum_j \xi_j(y) \] 其中,校正项,也就是平均失真为: \[ \xi_j(y) \triangleq \xi\left(q_j, q_j\left(u_j(y)\right)\right) \] 其与将 \(u_j(y)\) 转换为 \(q_j(y)\) 的第 \(j\) 个子量化器有关。可将其计算并存储与查找表中。
修正前后的概率分布函数如下图所示:
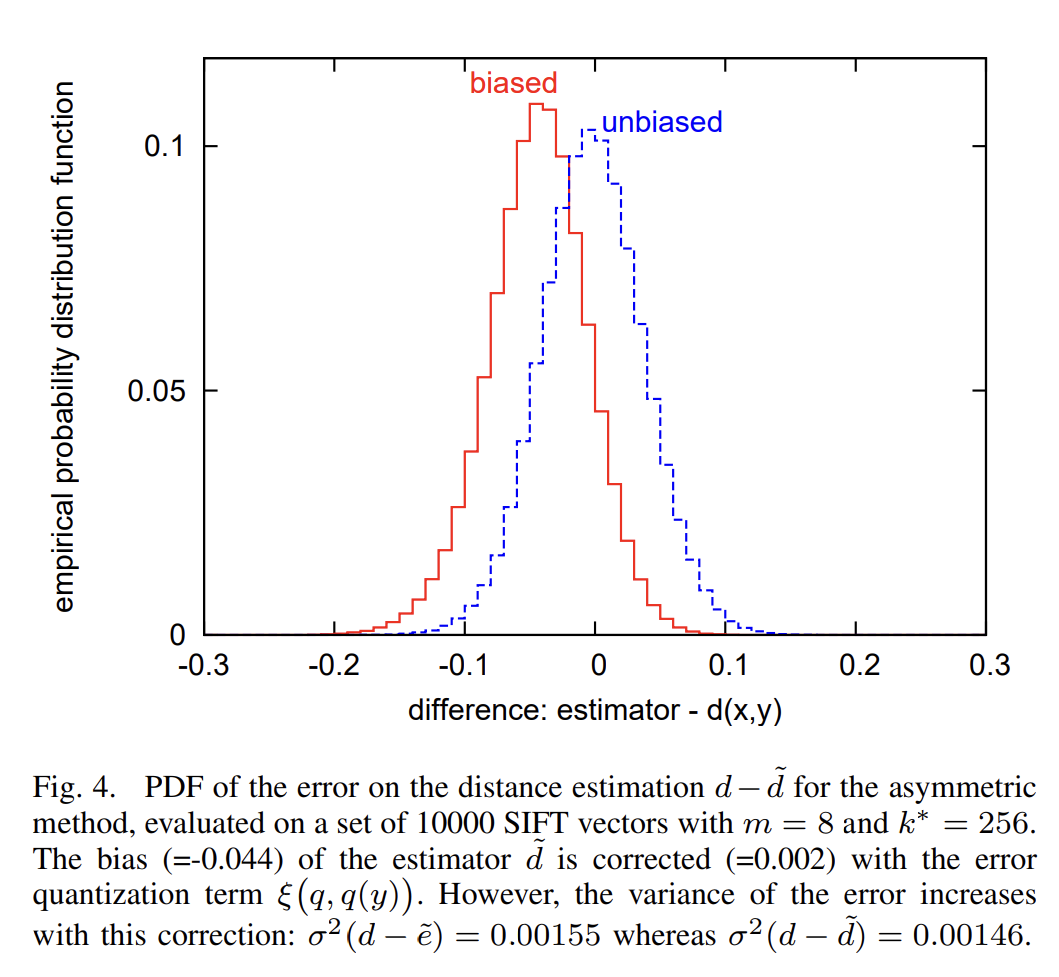
可以看出,校正后的版本偏差更小。然而,论文指出,在这种情况下,纠正偏差会导致估计量的更高方差,这是统计学中的常见现象。不过,在作者的实验中,观察到校正距离返回较差的结果。因此,建议在 ANN 查询过程中采用 ADC 计算距离。只有当我们对距离本身感兴趣时,修正后的版本才有用。
4. 非穷尽搜索
尽管使用 PQ 算法能减少内存占用,且通过查找表的方式让距离计算成本很低,但是其仍需要遍历聚类中心。
在 PQ 算法中,穷尽搜索(exhaustive search)指的是对于查询向量 \(x\),算法需要对每个子向量 \(u_j(x)\) 分别与子量化器的聚类中心(即子量化器的质心)进行比较,以确定每个子向量在相应子空间中的最近邻居。这个过程涉及到对每个子向量与所有聚类中心的距离计算,即使在实际应用中,可能只需要考虑每个子空间中的一小部分聚类中心。
在 PQ 算法中,查询向量 \(x\) 被分解为 \(m\) 个子向量,每个子向量 \(u_j(x)\) 通过一个子量化器 \(q_j\) 被量化为一个索引。然后,对于每个子向量,算法需要在相应的子空间中找到最接近的聚类中心,这通常涉及到对所有聚类中心的距离计算。这个过程在每个子空间中独立进行,最终通过组合所有子空间的结果来确定整个查询向量的最近邻居。
在大规模数据集上,这种穷尽搜索仍然是计算密集型的,因为它需要对每个查询向量的每个子向量进行多次距离计算。为了提高搜索效率,论文提出了结合倒排文件系统的方法,该方法通过使用粗粒度量化器进行数据分区,首先确定一个大概的搜索范围,然后在进行细粒度的 ANN 搜索,从而减少了实际搜索过程中需要进行的距离计算次数。这样,搜索过程就不再是对整个数据库的穷尽搜索,而是对预先确定的、数量较少的候选向量进行搜索。
4.1 粗粒度量化器与局部定义乘积量化器
粗粒度量化器 \(q_c\) 的聚类中心数 \(k'\) 需要根据数据集规模确定,对 SIFT 数据集,取值范围为 1000 ~ 1000000。首先使用粗粒度量化器将向量 \(y\) 编码为 \(q_c(y)\) ,定义残差向量为: \[ r(y)=y-q_{\mathrm{c}}(y), \] 其对应于沃罗诺伊单元中的偏移量。原始向量 \(y\) 则近似表示为: \[ \ddot{y} \triangleq q_{\mathrm{c}}(y)+q_{\mathrm{p}}\left(y-q_{\mathrm{c}}(y)\right) , \] 即由元组 \(\left(q_{\mathrm{c}}(y), q_{\mathrm{p}}(r(y))\right)\) 表示。这可以类比二进制数值的表示方式,粗量化器提供了显著的位,而乘积量化器的码则对应于不显著的位。
对查询向量 \(x\) 和数据库中向量 \(y\) ,距离 \(d(x, y)\) 估算为: \[ \ddot{d}(x, y)=d(x, \ddot{y})=d\left(x-q_{\mathrm{c}}(y), q_{\mathrm{p}}\left(y-q_{\mathrm{c}}(y)\right)\right) . \] \(q_{\mathrm{p}_j}\) 表示第 \(j\) 个子量化器,则可使用下面的分解来有效地计算这个距离估计值: \[ \ddot{d}(x, y)^2=\sum_j d\left(u_j\left(x-q_{\mathrm{c}}(y)\right), q_{\mathrm{p}_j}\left(u_j\left(y-q_{\mathrm{c}}(y)\right)\right)\right)^2 . \] 乘积量化器是在从学习集收集的残差向量集上学习的。尽管粗粒度量化器将向量量化到不同的索引,但由此产生的残差向量被用来学习一个唯一的乘积量化器。我们假设,当残差在所有沃罗诺伊单元上的分布被边缘化时,相同的乘积量化器仍然准确。这可能比为每个沃罗诺伊单元学习和使用不同的乘积量化器的方法得到的结果要差。然而,这样做在计算上会很昂贵,并且需要存储 \(k'\) 个乘积量化器码本,即 \(k' \times d \times k^{*}\) 个浮点值,对于 \(k'\) 的常见值来说,这在内存上是不可行的。
4.2 索引结构
使用粗粒度量化器来实现倒排索引。倒排索引可看作一个 list 数组:\(\mathcal{L}_1,…,\mathcal{L}_{k'}\) 。若 \(\mathcal{Y}\) 是需要索引的数据集,粗粒度量化器 \(q_c\) 的聚类中心 \(c_i\) 的对应列表是 \(\mathcal{L}_i\) ,其存储了: \(\mathcal{y} \in \mathcal{Y} : q_c(\mathcal{y} = c_i)\) 。
在倒排列表 \(\mathcal{L}_i\) 中,向量 \(y\) 的一个条目包括向量标识符和量化残差 \(q_p(r(y))\) :

标识符字段是由于倒排文件结构造成的开销。根据要存储的向量的性质,标识符并不一定是唯一的。例如,为了通过局部描述符描述图像,图像标识符可以替代向量标识符,即同一图像的所有向量具有相同的标识符。因此,一个 20 位的字段就足以从一百万的图像数据集中识别一个图像。
4.3 查询算法
倒排索引是实现非穷尽查询的关键。给定查询向量 \(x\) ,倒排索引根据估计的距离提供了一个子集 \(\mathcal{Y}\) :只有对应于 \(q_c(x)\) 的列表 \(\mathcal{L}_i\) 需要被扫描。
由于 \(x\) 与其最近邻不一定量化到一个单元,查询 \(x\) 被分配给 \(w\) 个索引,而不是只有一个索引,这些索引对应于 \(q_c\) 的码本中 \(x\) 的 \(w\) 个最近邻居。扫描所有相应的倒排表。多重赋值不应用于数据库向量,因为这会增加内存使用。
插入和查询过程如下图所示: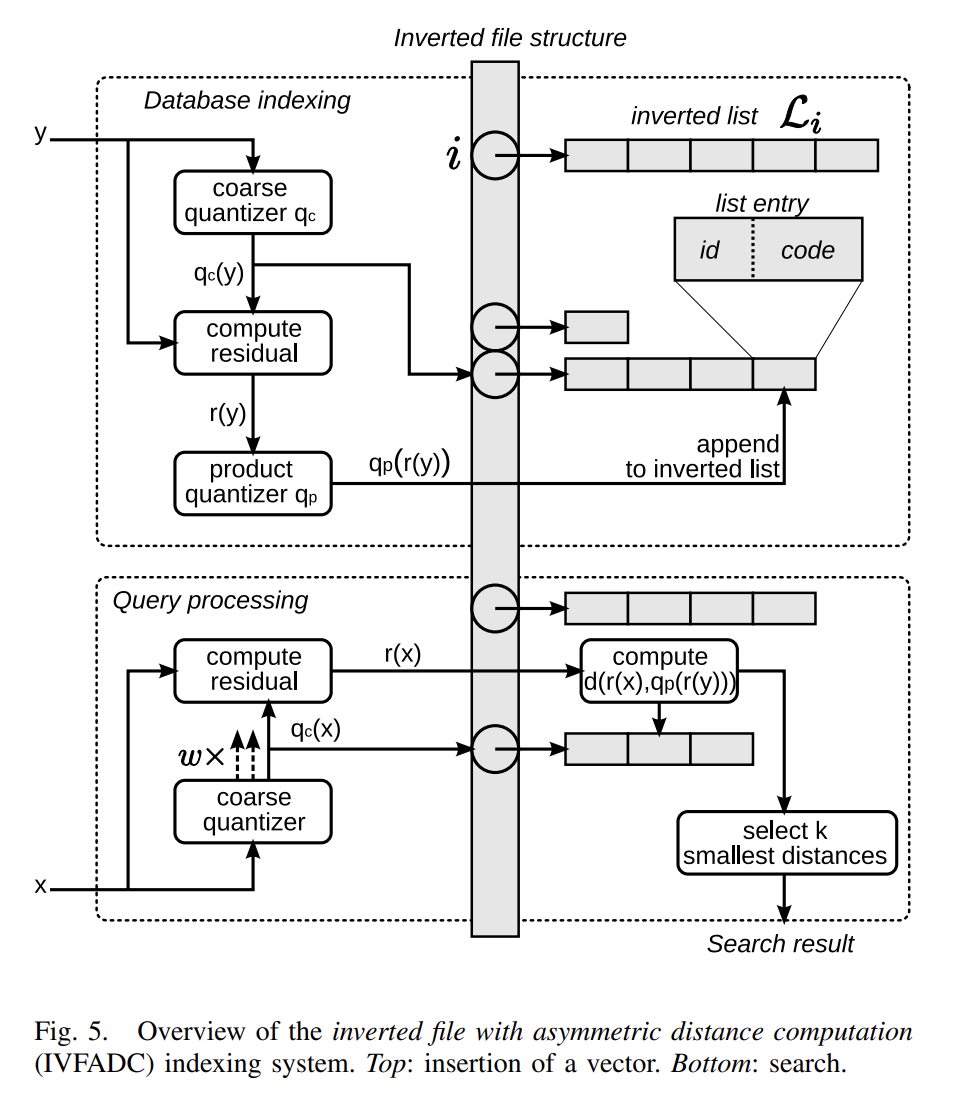
算法流程解释如下:
插入算法

查询算法

5. 总结
本文引入了乘积量化用于近似最近邻搜索。我们的紧凑编码方案提供了对欧几里得距离的准确近似。此外,它与倒排文件系统相结合,避免了穷尽搜索,从而实现了高效率。我们的方法在搜索质量和内存使用之间的权衡上显著优于现有技术。对于 SIFT 和 GIST 图像描述符的实验结果非常出色,并且表明,基于我们对描述符设计先验知识的组件分组可以进一步改善结果。我们的方法在 20 亿个向量的数据集上验证了其可扩展性。